"How far can you listen?"

Apart from being gibberish, it's a valid question, and short for: What is the expected detection range for my hydrophone for a given sound source? - Valuable information when choosing deployment density and pattern.

Consider the NOAA mid-Atlantic acoustic monitoring setup:

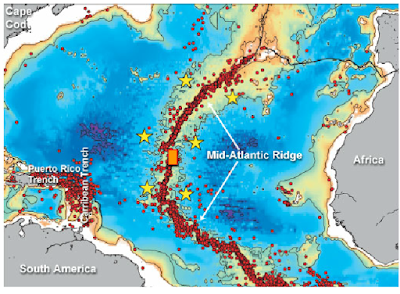Figure1: Image from an earthquake survey. The stars indicate positions of hydrophones.

If a signal is picked up by more than one hydrophone (stars on the map), the relative signal strengths will provide some clue to the distance of the source. For a good 2D position estimation at least three hydrophones have to pick up the signal. So when planning surveys it is important to get the distance between the hydrophones right. It's an optimisation between the cost of too many hydrophones, and the potential for missed detections with too few hydrophones.

So how do you find out how big your hydrophone's detection range is? Simple spherical approximation is likely to be far from actual values, even if correction for attenuation is applied as well (National Physical Laboratory has a great article on this). But even this simple approach will become fairly involved, and not very accurate.
Software like dBSea can help. It takes many factors (variable speed of sound, complex attenuation and bathymetry) into account, and even though it was never meant to be used to asses hydrophone detection range, it can be used in "reverse-mode" for this exact purpose.
Lets assume that a hydrophone has the self-noise levels seen in Figure 2 (dotted line). This noise floor represents the lowest pressure levels that the hydrophone can detect, it denotes a sort of new baseline for what constitutes as zero noise.

Figure 2: Noise floor/self noise of the "Soundtrap 300" (dottet line), and that converted to a sound source (solid line).

By subtracting the self noise values from the maximum sound pressure level possible at the deployment depth (I'll call that maxSPL, see Figure 3) a value for the available measuring dB-range can be established (Figure 2).

Figure 3: The maximum sound pressure (for tones) are limited by by ambient pressure as sound waves cannot be sustained in a vacuum.

Now comes the tricky part; to find out how far the hydrophone can "hear", I convert it to a sound source with its frequency-dependent dB-range at its output level (as per Figure 2). When a source like this is modelled in dBSea the resultant model will map how much below maxSPL a source in the environment can be, and still be detected at the given range.

Figure 4: Range map for our hydrophone for detecting fin whale in sea-state 4, assuming no ship traffic... Notice the 3D colour plot, a new feature coming out in dBSea soon.

In the above figure the listening range of our hydrophone is depicted. It's weighted for detection of fin whale (from this blog post), in the somewhat windy and wavy condition of "Sea State 4". I haven't included ship noise (It would have to be an average background noise addition), and I don't know about the directionality of the fin whales call.
So really what we have in Figure 4, is the range at which we can expect to detect a fin whale that's being as loud as possible.

Note: For technical readers that wonder why the scale only goes to 34 dB in Figure 4. It is so because the low frequencies of the sound weighting (central freq. 250 Hz), have low attenuation, ~0.006 dB/km, so spherical spreading loss accounts for much of what's visible in Figure 4. A zoomed in picture on the source would reveal values up to the threshold.

The knowledge we gain from this exercise is quite profound; for monitoring fin whales in the Rockall Trough (the deep "channel" running SW-NE in Figure 4), the spacing between hydrophones can be much greater than over the two banks flanking it, the most effective set-up is far from a regular grid.
Another key insight provided is that similar received levels at the hydrophone don't represent equidistant sources, as sources in the Rockall Trough can be further away than ones on the banks, but still yield similar received levels.

Looking at the frequency-dependent attenuation can help find the source distance when it is otherwise obscure (i.e. the signal being detected on fewer than three receivers) - I'm working on a post on this subject, so stay tuned for that!